Both Triangular And Quadrilateral Is Equal To 360 Degrees . To find unknown angles in a. ∠p + ∠q + ∠r + ∠s = 360º. the reason interior angles in a quadrilateral sum to 360° is because a quadrilateral can be divided into two triangles. — answer link. the sum of the interior angles of any quadrilateral is 360°360°. So the general rule is: Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: A quadrilateral can be divided with a diagonal into two triangles each with an interior angle sum of 180^@ it really depends upon. consider a quadrilateral pqrs. Consider triangle pqs, we have, ⇒ ∠p +. Angles in a complete turn and angles in triangles. according to the angle sum property of a quadrilateral, the sum of all the four interior angles is 360 degrees. We can prove this using the angle sum of a triangle. A complete turn is a 360˚ rotation.
from www.mathplanet.com
— answer link. A complete turn is a 360˚ rotation. consider a quadrilateral pqrs. A quadrilateral can be divided with a diagonal into two triangles each with an interior angle sum of 180^@ it really depends upon. We can prove this using the angle sum of a triangle. Consider triangle pqs, we have, ⇒ ∠p +. To find unknown angles in a. Angles in a complete turn and angles in triangles. So the general rule is: the sum of the interior angles of any quadrilateral is 360°360°.
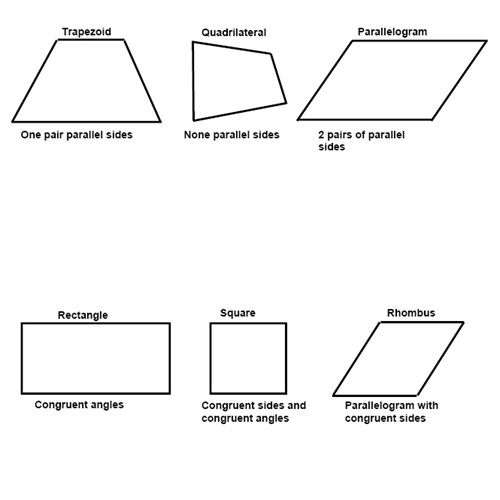
Quadrilaterals, polygons and transformations (PreAlgebra, Introducing
Both Triangular And Quadrilateral Is Equal To 360 Degrees Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: the reason interior angles in a quadrilateral sum to 360° is because a quadrilateral can be divided into two triangles. according to the angle sum property of a quadrilateral, the sum of all the four interior angles is 360 degrees. Angles in a complete turn and angles in triangles. A complete turn is a 360˚ rotation. We can prove this using the angle sum of a triangle. consider a quadrilateral pqrs. To find unknown angles in a. Consider triangle pqs, we have, ⇒ ∠p +. ∠p + ∠q + ∠r + ∠s = 360º. — answer link. Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: So the general rule is: A quadrilateral can be divided with a diagonal into two triangles each with an interior angle sum of 180^@ it really depends upon. the sum of the interior angles of any quadrilateral is 360°360°.
From www.media4math.com
Student Tutorial Geometry Basics Quadrilateral Basics Media4Math Both Triangular And Quadrilateral Is Equal To 360 Degrees ∠p + ∠q + ∠r + ∠s = 360º. the reason interior angles in a quadrilateral sum to 360° is because a quadrilateral can be divided into two triangles. Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: We can prove this using the angle sum of a. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From www.youtube.com
5.12 Properties of Quadrilaterals and Triangles Basic Maths GCSE Core Both Triangular And Quadrilateral Is Equal To 360 Degrees — answer link. Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: Angles in a complete turn and angles in triangles. A quadrilateral can be divided with a diagonal into two triangles each with an interior angle sum of 180^@ it really depends upon. the reason interior. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From www.mathswithmum.com
Angles in Quadrilaterals Maths with Mum Both Triangular And Quadrilateral Is Equal To 360 Degrees Angles in a complete turn and angles in triangles. according to the angle sum property of a quadrilateral, the sum of all the four interior angles is 360 degrees. — answer link. consider a quadrilateral pqrs. So the general rule is: Consider triangle pqs, we have, ⇒ ∠p +. Each time we add a side (triangle to. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From mathmonks.com
Quadrilateral Definition, Properties, Types, Formulas, Examples Both Triangular And Quadrilateral Is Equal To 360 Degrees Angles in a complete turn and angles in triangles. Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: — answer link. We can prove this using the angle sum of a triangle. the sum of the interior angles of any quadrilateral is 360°360°. consider a quadrilateral. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From slideplayer.com
Types of Quadrilaterals ppt download Both Triangular And Quadrilateral Is Equal To 360 Degrees — answer link. Angles in a complete turn and angles in triangles. We can prove this using the angle sum of a triangle. consider a quadrilateral pqrs. the reason interior angles in a quadrilateral sum to 360° is because a quadrilateral can be divided into two triangles. Each time we add a side (triangle to quadrilateral, quadrilateral. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From www.bbc.co.uk
Angles in triangles and quadrilaterals KS3 Maths BBC Bitesize BBC Both Triangular And Quadrilateral Is Equal To 360 Degrees according to the angle sum property of a quadrilateral, the sum of all the four interior angles is 360 degrees. Angles in a complete turn and angles in triangles. Consider triangle pqs, we have, ⇒ ∠p +. ∠p + ∠q + ∠r + ∠s = 360º. the sum of the interior angles of any quadrilateral is 360°360°. Each. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From manualfixfaber.z19.web.core.windows.net
Angles Inside A Quadrilateral Both Triangular And Quadrilateral Is Equal To 360 Degrees ∠p + ∠q + ∠r + ∠s = 360º. Angles in a complete turn and angles in triangles. So the general rule is: according to the angle sum property of a quadrilateral, the sum of all the four interior angles is 360 degrees. To find unknown angles in a. Consider triangle pqs, we have, ⇒ ∠p +. the. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From ck12.org
Understanding the Angle Measures of Quadrilaterals CK12 Foundation Both Triangular And Quadrilateral Is Equal To 360 Degrees A quadrilateral can be divided with a diagonal into two triangles each with an interior angle sum of 180^@ it really depends upon. — answer link. Angles in a complete turn and angles in triangles. consider a quadrilateral pqrs. To find unknown angles in a. the reason interior angles in a quadrilateral sum to 360° is because. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From catman3000.hubpages.com
What is the sum of all the angles in a 4 sided shape (angles in a Both Triangular And Quadrilateral Is Equal To 360 Degrees A complete turn is a 360˚ rotation. Angles in a complete turn and angles in triangles. according to the angle sum property of a quadrilateral, the sum of all the four interior angles is 360 degrees. A quadrilateral can be divided with a diagonal into two triangles each with an interior angle sum of 180^@ it really depends upon.. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From www.youtube.com
Sum of all angles in a quadrilateral is equal to 360 YouTube Both Triangular And Quadrilateral Is Equal To 360 Degrees A complete turn is a 360˚ rotation. A quadrilateral can be divided with a diagonal into two triangles each with an interior angle sum of 180^@ it really depends upon. the sum of the interior angles of any quadrilateral is 360°360°. To find unknown angles in a. according to the angle sum property of a quadrilateral, the sum. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From www.ck12.org
Quadrilaterals and Angles CK12 Foundation Both Triangular And Quadrilateral Is Equal To 360 Degrees Angles in a complete turn and angles in triangles. A complete turn is a 360˚ rotation. ∠p + ∠q + ∠r + ∠s = 360º. So the general rule is: Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: A quadrilateral can be divided with a diagonal into two. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From www.animalia-life.club
Types Of Quadrilaterals Both Triangular And Quadrilateral Is Equal To 360 Degrees A complete turn is a 360˚ rotation. consider a quadrilateral pqrs. ∠p + ∠q + ∠r + ∠s = 360º. — answer link. the reason interior angles in a quadrilateral sum to 360° is because a quadrilateral can be divided into two triangles. Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From www.youtube.com
Sum of all angles in quadrilateral is 360° (Theorem and Proof) YouTube Both Triangular And Quadrilateral Is Equal To 360 Degrees A complete turn is a 360˚ rotation. So the general rule is: ∠p + ∠q + ∠r + ∠s = 360º. Angles in a complete turn and angles in triangles. the sum of the interior angles of any quadrilateral is 360°360°. Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From www.cuemath.com
Quadrilaterals Definition Meaning Types Quadrilateral Shape Both Triangular And Quadrilateral Is Equal To 360 Degrees We can prove this using the angle sum of a triangle. the reason interior angles in a quadrilateral sum to 360° is because a quadrilateral can be divided into two triangles. A quadrilateral can be divided with a diagonal into two triangles each with an interior angle sum of 180^@ it really depends upon. ∠p + ∠q + ∠r. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From learningschoolgraciauwb.z4.web.core.windows.net
Types Of Quadrilateral Hierarchy Both Triangular And Quadrilateral Is Equal To 360 Degrees the sum of the interior angles of any quadrilateral is 360°360°. — answer link. according to the angle sum property of a quadrilateral, the sum of all the four interior angles is 360 degrees. Angles in a complete turn and angles in triangles. A quadrilateral can be divided with a diagonal into two triangles each with an. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From brainly.com
The sum of the measures of the four angles of a quadrilateral is 360 Both Triangular And Quadrilateral Is Equal To 360 Degrees So the general rule is: Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: To find unknown angles in a. ∠p + ∠q + ∠r + ∠s = 360º. consider a quadrilateral pqrs. Angles in a complete turn and angles in triangles. the sum of the interior. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From www.mathplanet.com
Quadrilaterals, polygons and transformations (PreAlgebra, Introducing Both Triangular And Quadrilateral Is Equal To 360 Degrees Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total: Consider triangle pqs, we have, ⇒ ∠p +. A complete turn is a 360˚ rotation. Angles in a complete turn and angles in triangles. So the general rule is: We can prove this using the angle sum of a triangle.. Both Triangular And Quadrilateral Is Equal To 360 Degrees.
From aumannclassroom.weebly.com
Triangles and Quadrilaterals Mr. Aumann's Class Both Triangular And Quadrilateral Is Equal To 360 Degrees the sum of the interior angles of any quadrilateral is 360°360°. Angles in a complete turn and angles in triangles. We can prove this using the angle sum of a triangle. Consider triangle pqs, we have, ⇒ ∠p +. A quadrilateral can be divided with a diagonal into two triangles each with an interior angle sum of 180^@ it. Both Triangular And Quadrilateral Is Equal To 360 Degrees.